Random insights on lead-acid battery theory

Overview

This is a collection of insights regarding lead-acid batteries, in particular those sealed batteries that are used in UPSes. Had it not been for my failed attempts to get a decent battery for my UPS, none of this would have been written. It was only when I asked myself why the UPS doesn’t maintain power nearly as long as I expected that I started to learn more about these batteries.

Batteries is far away from anything I do for a living. This is definitely not my expertise. Please keep that in mind. But as it turns out, there’s a lot to know about them.

Well, I think I’ll take that back: After a lot of playing with these batteries, my conclusion is that knowledge doesn’t help much. Run a test, see how long the battery holds up your computer, and that’s it. There doesn’t seem to be anything smarter to do.

There’s probably only one important thing to know about them: They should be fresh. That’s hardly new, and yet, that’s probably the bottom line. Lead-acid batteries discharge by themselves over time, and when they reach a certain level of discharge, they get damaged. Also, the discharge rate depends a lot on temperature. So a battery that has been stored in a hot place somewhere in a distant country for over a year is probably no good candidate for your UPS. The manufacturer’s timestamp is everything: It starts to seem to me that most batteries were more or less the same on the day that they left the factory. The difference is how much damage they caught during storage.

For a concise technical background, I recommend reading Power Sonic’s Technical Manual.

So without further ado, let’s go through my findings, in more or less random order.

A 7AH battery doesn’t really give 7AH

With lead-acid batteries, 7AH doesn’t meas 7A for 1 hour. Or 3.5A for 2 hours. Or any other combination, except for 0.35A for 20 hours. More about that below.

The amount of charge (and energy) that a lead-acid battery supplies until it’s discharged depends dramatically on the discharging current. The capacity printed on the battery is given for a 20-hours discharge, or using the jargon, 0.05C. That “C” is 7 taken from the 7AH figure, so 7AH are obtained if the discharge current is 0.35A. For larger currents, expect much less energy out of the battery.

This phenomenon is approximated by Peukert’s Law.

For example, my specific case: The load is 70W (at 142VA) according to the UPS itself. I’ll assume that the low power factor thing can be ignored, i.e. that the fact that the VA figure is twice the consumed power makes no difference. This low power factor is natural to switching power supplies, as they draw more current when the voltage is low, so their behavior is far from a plain resistor (unless specifically compensated to mitigate this effect). I’ll also assume that the UPS is 100% efficient on its voltage conversion, which is complete rubbish, but for the heck of it.

So for two 12V batteries in series it goes 70W/24V =~ 2.9A, which is about 0.4C (2.9 / 7 =~ 0.4). A ballpark figure can be taken from Figure 4 in Power Sonic’s Technical Manual, showing that the voltage starts to drop after about an hour, and reaches the critical value somewhere after an hour and a half. Note that I have different batteries.

Also from Table 2 of the same Manual, we have that the actual capacity of a 7AH battery, when drained with a 4.34A current, is 4.34AH (one hour). The current is higher than 2.9A, but given that the UPS isn’t really 100% efficient, it’s likely that the real discharge current is closer to 4A than to 2.9A. So that explains why the UPS said 1:12 hours when I updated the battery replacement date.

Many battery manufacturers supply datasheets with Discharge Characteristics Curves. Even better, if there are tables with Constant Current Discharge Characteristics (also referred to as F.V / Time specification). See Ritar’s datasheet for RT1270, for example. The numbers inside this table are the constant currents for each discharging scenario. Each row is the final voltage (F.V) per cell that is reached in this scenario, and each column represents the time it takes to reach this voltage.

It’s not clear at which voltage the UPS decides to stop discharging. Even though 1.60V per cell seems to be a recurring number in datasheets for the game over.  And on the other hand, I’ve repeatedly seen 0.35A (i.e. 0.05C) paired with 1.75V and 20 hours discharge in those F.V / Time tables. So it’s not really clear. Anyhow, finding a number that is similar to the intended current in the table can give an idea on how long the battery is supposed to last.

Obviously, different batteries behave differently on higher currents. I couldn’t find data on my “Bulls Power” batteries. So maybe they could meet the 7AH specification for a 20-hours discharge, and then perform really poorly with higher, real-life currents. No way to know for sure.

So what is the state of the battery after it has been discharged with less than 7AH? It’s still charged, as a matter of fact. A rapid discharge, which yields less than the full capacity is healthy for the battery. It’s when the full capacity is utilized with a slow discharge pattern that the battery can be damaged if it stays in that state for a long while.

Charging a lead-acid battery

There are in fact several ways to charge a lead acid battery (for example, this), but the common way to charge a battery is to feed it with a current of 0.3C (2.1A for a 7AH battery) until the voltage rises to above a threshold. Or to set a constant voltage (with a current limit) and charge until the current goes below a certain level. Then comes the second phase, which is the slow charging to 100%.

When the battery is full, a floating voltage should be applied to the battery. Each battery specifies its own preferred floating voltage, but they all land at around 13.5-13.8V. This is the correct way to maintain a fully charged battery: A small charging current compensates for the battery’s inherent discharge (typically around 0.001C, i.e. 7 mA for a 7AH battery), and the battery remains fully charged in a way that is best for its health.

Battery manufacturers usually state something like 10% discharge for 90 days or so. This corresponds to about 0.000046C, or ~0.3 mA for a 7AH battery. But in this scenario, the battery discharges against its own voltage, and not the elevated floating voltage (does it matter?).

Knowing the battery’s charge level

How does one estimate how much energy a lead-acid battery has? The answer is unpleasant, yet simple: There is really no way to measure it from the battery electronically. After reading quite some material on the subject, that became evident to me: There are plenty of papers describing exotic algorithms for estimating a battery’s health and charge level, and their abundance and variety proves that there’s really no way to tell, except for draining it.

Maybe the first question should have been: What is consumed when the battery gets discharged? For one, sulfuric acid reacts with the lead plates and become lead sulfate. When there’s no acid left, the battery is done. On the other hand, the lead plates themselves might deteriorate in the process. This can happen relatively early if the lead plates are partly damaged because of previous use (or abuse).

There is one way to measure the charge level that is considered reliable, which is measuring the open circuit voltage (OCV) after the battery has been disconnected for a while (some say a few hours, battery manufacturers typically require 24 hours). Letting the battery rest allows it to reach a chemical equilibrium, at which point the voltage reflects its charge level. This is surely true for a fresh battery, because the OCV reflects the specific gravity of the electrolyte, that is the concentration of the sulfuric acid.

As for batteries with some history, the picture is less clear, and I haven’t managed to figure out if the OCV voltages remain the same, and if the voltage vs. charge percentage relate to the original charge capacity, or the one that is available after the battery is worn out. The OCV measurementt covers the charge level in the sense of how much acid there’s left to consume, but will the lead plates hold that long?

For example, Power Sonic claims that the OVC goes from 1.94V/cell to 2.16V/cell for 0% to 100% charge respectively. As a 12-volt battery has 6 cells, this corresponds to 11.64V to 12.96V. These figures are quite similar to those presented by another manufacturer.

But what does 100% charge mean? 7AH or as much as is left when the battery has worked for some time? My anecdotal measurement of the batteries I took out from the UPS was 12.99V after letting them rest. In other words, they presented a OCV voltage corresponding to 100% charge, even though they had much less than 7AH.

So how does a UPS estimate the remaining runtime? Well, the simple way is to let the battery run out once, and there you have a number. Clearly, Smart UPS uses this method.

Are there any alternatives? In theory, the UPS could let the battery rest for 24 hours, and measure its OCV. This is possible, because most of the time the UPS doesn’t need the battery. But even my anecdotal measurement shows that a 100% charge-like reading doesn’t mean much.

For other types of batteries (Li-ion in particular), measuring the current on the battery, in and out (Coulomb Counting), gives an idea on how much charge it contains. This doesn’t work with lead acid batteries, because the recommended way to maintain a standby battery, is to continuously float charge it. That means holding a constant voltage (say, 2.25V per cell, that is 13.5V for a 12V battery, or 27V on a battery pair, as in SmartUPS 750).

As this voltage is higher than the OCV at rest, this causes a small trickle current (said to be about 0.001C), which compensates for the battery’s self discharge. Even if it overcharges the battery slightly, the gases that are released are recycled internally in a sealed battery, so there’s no damage.

Hence the recommended strategy for charging a lead-acid battery is to charge it quickly as long as its voltage / current pair indicates that it’s far from being fully charged, and then apply a constant, known and safe voltage. This allows it to charge completely slowly, and then maintain the charge without any risk for overcharging. Odds are that this is what the UPS does.

But that makes Coulomb Counting impossible: During the float charge phase (that is, virtually all the time) the current may and may not actually charge the battery.

Measuring the discharging curve

Being quite frustrated by bad batteries, I decided to go for a more direct approach: Instead of taking my computer down and pushing the battery into the UPS each time, I thought it would be easier and more informative to run a discharging test: I used my old Mustek 600 UPS to charge the battery, and then discharged it through a (cheap) 55W light bulb for a car’s headlight (which is intended for 12V of course). With this, I ran a classic lab experiment, recording voltage and current as a function of time. Like a school lab.

The first step is to charge the battery of course. I’ve discussed this topic briefly above, but what about my Mustek’s UPS? It takes a very easy and slow approach: With a partly discharged battery, it starts with an initial charging current of 0.4–0.35 A. This current goes slowly down as the battery’s voltage rises. The voltage goes up very slowly from 12.8V and eventually stabilizes at a voltage around 13.5-13.6V (depends on the battery). Charging a battery to a decent level takes 7 hours, but I went for a 24 hours charge before running a discharging test. Just to make sure the battery was really fully charged.

By the way, the Mustek UPS charges even when not powered on (but connected to power). When disconnected from power, no charging occurs.

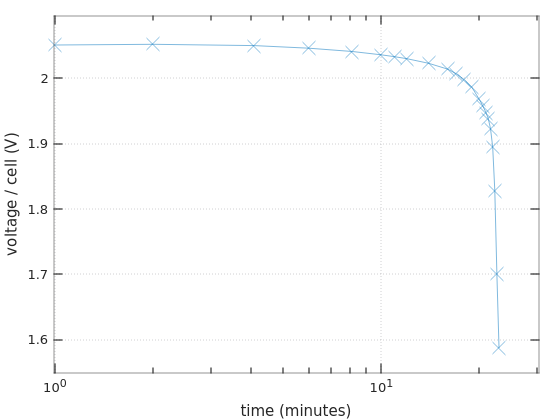
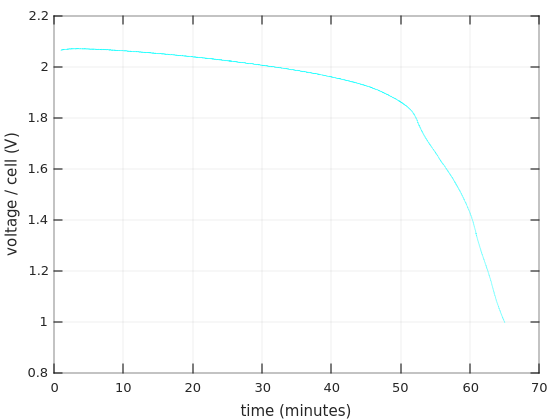
Now to the interesting part: The discharging of the batteries. I made several tests, and they all yielded the same results, more or less. In all of these, I made accurate voltage measurements (with a Fluke) as a function of time. This is the plot of the last experiment I did, with a logarithmic x-axis, each ‘x’ mark on the plot is a measurement:

This experiment was done on one of the Bulls Power batteries.

I measured the current throughout the session: The light bulb drew 4.00 A in the beginning (corresponding to ~48W), and the currents remained above 3.8A during the first 20 minutes. So this can be considered a 0.55C discharge.

The first thing to note is that the graph fits the discharge curve for Ritar’s RT1270 for 0.55C during the first 18-19 minutes: The voltage goes down gradually, and drops about 0.04V/cell during the first 10 minutes. On the next 8-9 minutes, the voltage drop is about 0.05V/cell, also following Ritar’s curve.

But then it’s quickly downhill, strongly diverting from the expected graph. The battery collapses quickly at this point. I haven’t found a single reference to this behavior, but I suppose that it’s a result of aging. And/or deep discharge during storage.

Is this consistent with the fact that this battery held for 9 minutes in the UPS, along with one that behaves roughly the same? Maybe. The UPS reported a power consumption of 105W in that situation, so if I’ll assume 90% power efficiency, we have a current of 105 * (1 / 0.9) / 24 = 4.86A ≈ 0.7C. That’s somewhere between the graph for 0.55C and 1C. So with the steeper discharging curve of this case, it’s actually possible that the collapse began much earlier.

Other random takeaways:

• With this battery, it doesn’t matter so much at which voltage the UPS powers itself off. The last part’s slope is so steep, so it’s a matter of 30 seconds this way or another.
• A 55W light bulb is blinding and heating. Be sure to have it fixed in a way that prevents it from heating the battery and also make sure  that it’s literally out of sight, and that no visual contact will be needed with it as long as the experiment runs.
• Check the crocodiles’ or easy-hook’s resistance. In particular crocodiles can have a high an unstable resistance (0.1Ω is high in this context, because it causes a voltage drop of 0.4V).
• As it says in many information sources, lead batteries recover after a discharging session after some time of rest: After a day, I connected the battery to the bulb, and it began discharging at 11.8V, and falling rapidly.

Discharging curves, round #2

The saga went on, and I tell it in detail in the other post. The quick summary is: Being unhappy with the Bull batteries, I bought a pair of batteries from a company named Afik, and put them in the UPS. The results weren’t really impressing with these either, so I decided to replace the Afik batteries with something else. Eventually, I ended up with a pair of Vega Power batteries.

Unfortunately, I didn’t make any measurements on the Afik batteries before putting them in the UPS, mainly because I thought they would work, and end of story. So as things turned out, I obtained the discharging curve from the new Vega Power batteries before putting them in the UPS, and then I did the same thing with the Afik batteries only after they had been in the UPS for a few months.

This time I created an automatic test setting that allowed two readings per second, so the curves are more accurate and detailed.

Note to self: See new-computer/ups/lead acid batteries/discharge-tests-2/.

I used the same light 55W light bulb, which drew 4.0A at the beginning of the discharging test, and then went down slowly to about 3.5A towards the end of the test. More or less constant current, that is.

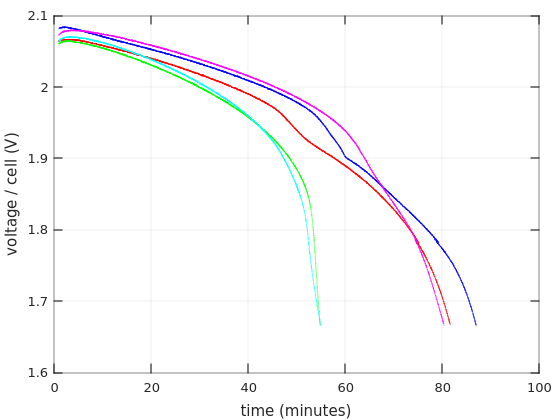
The colors of the curves in the graphs below represent which test they belong to:

• Red: Vega Power battery #1.
• Blue: Vega Power battery #2, first test.
• Magenta: Vega Power battery #2, second test.
• Green: Afik battery #1.
• Cyan: Afik battery #2.

Evidently, I obtained a curve from Vega Power battery #2 twice: Once after charging for ~24 hours (from as it came from the shop) with the Mustek UPS, and the second time after a total of ~48 hours from the state of the previous discharging session. The graphs below might imply that I got these two measurements swapped, but no, there’s no mistake about this.

Vega Power battery #1 was charged during 26 hours (from its initial state from the shop), and then 18 hours with a brief pause between the two charging sessions.

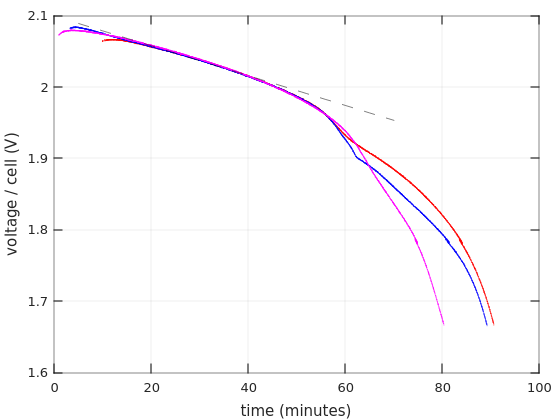
So to the first graph. Time in minutes on the X axis, and voltage per cell on the Y axis.

The curves begin one minute after discharging starts, and stop when the battery reached 10.0V (with 6 cells in the battery, that’s 1.67V / cell). I’ll show more details below about the first minute. As for choosing 1.67V as the end for discharging: The graphs for charging current around 0.55C often go this low in datasheets, so I suppose this shouldn’t damage the battery.

The first and obvious thing one can see is that the Afik batteries held shorter than the Vega Power batteries: 55 minutes vs. 80-87 minutes. That’s consistent with the fact that the Vega Power lasted longer in the UPS.

But as I’ve written in that other post, the UPS started to panic-beeping after 7:30 minutes with the Afik batteries, and then kept power up for another 15 minutes. Why did that happen? There’s nothing in the green nor cyan curves that offers a clue for the reason to the early panic. On the other hand, it’s evident that these batteries lost voltage quite rapidly after about 40 minutes, possibly going into “deep discharge”. That said, they didn’t collapse nearly as quickly as the Bull Power batteries. So there are definitely different levels of junk.

As for the Vega Power batteries, they performed surprisingly well on these tests. The shortest run was 80 minutes. Taking a gross average of 3.75A as the current, that means that the battery gave 5AH. Quite impressive. Also, according to Ritar’s datasheet for RT1270, that battery will reach 1.85V/cell after one hour if a current of 3.321A is drawn from it. Vega Power got to that region after 70 minutes with a higher current.

So the question is why the UPS started panicking after 28 minutes and cut the power very soon after that. Indeed, the current that is drawn from the batteries was higher inside the UPS. But why that sudden cut? Does it have to do with the curves’ bending at around 1.96V?

In fact, the reason that I repeated the first discharging test on Vega Power #2 (in blue) was that sharp bend. To my surprise, the bend went away on the second test (in magenta), but the battery reached the 1.67V point 7 minutes earlier (after a 48 hours charging). Why? Don’t know. Lead acid batteries are not supposed to have any memory.

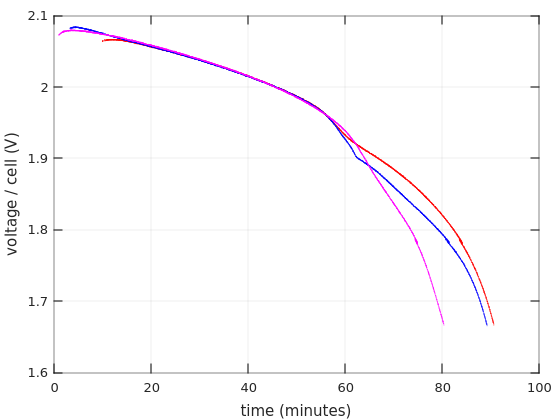
In the next graph, I’ve removed the curves for the Afik batteries, and left only Vega Power’s curves. In addition, I’ve shifted the positions of these curves in the X axis. Namely, I delayed Vega #1′s curve by 9 minutes, and Vega #2′s first test’s curve 2:15 minutes. And we get this:

So it’s evident that both batteries ran according to an accurate discharging pattern for at least 45 minutes, and then things happened. Is this the start of “deep discharge”? Does this mean that discharging the batteries below 1.95V is a bad idea? Maybe this is what my UPS thought, and accordingly stopped after 28 minutes (which could be the same point, as it probably drew more current than this test).

Doesn’t the part where all three curves overlap look a little linear? I’ll come back to that below.

It also looks like the shifting I made in the X axis compensates for differences in the initial charging level. If that’s true, the charging levels of Vega Power #2 were nearly the same in both tests (slightly more charge after the second, 48-hours, charging session). But if so, why did this battery reach 1.67V faster on the second round?

And why was Vega Power #1 significantly less charged after a super-long charging session? Maybe an issue with the Mustek UPS?

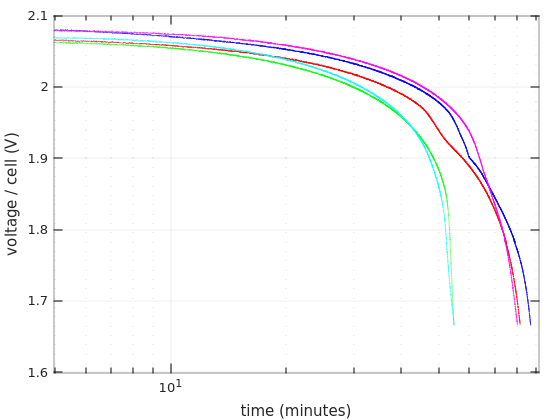
The third graph is the same as the first, but with logarithmic X-axis.

The interesting thing about this representation is that it’s comparable with the curves that appear in some batteries’ datasheets. It’s quite evident that these curves are similar to those that are usually given for 0.55C.

The bends of the blue and red curves are more evident on this graph. Recall that they were obtained during the first tests of each of the Vega Power batteries. The pretty curve in magenta is the second run of Vega Power #2.

Finally, I discharged Afik battery #2 down to 1V, which is considered a damaging thing to do. But who cares, I have no plans for this battery anyhow. So here’s the curve:

Note that this is the same test and same curve as shown above, only that I display it in full here.

Transient responses

So far I’ve been looking at the curves during the actual discharging phase. But some possibly interesting things happen before and after that.

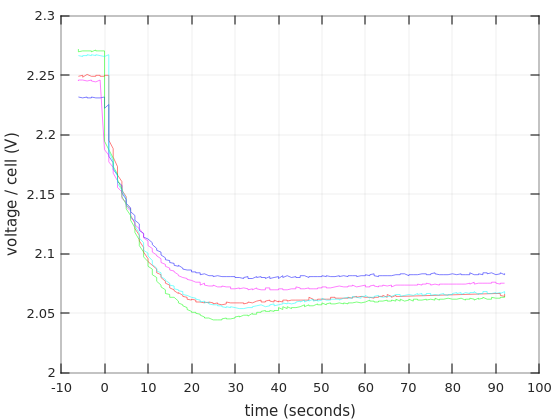
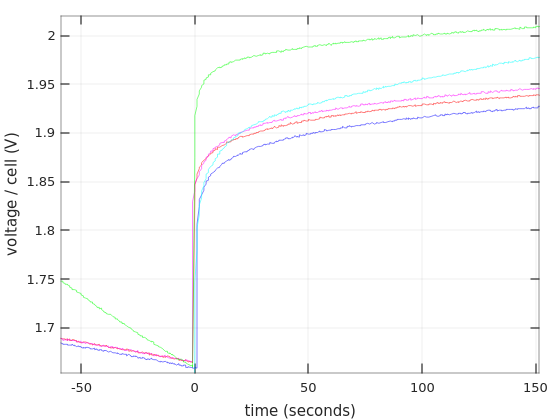
So first, what happens when the discharging begins:

Surprise, surprise, there’s an undershoot. Why? I’m tired of trying to even speculate. But it’s definitely a thing. And by the way, the initial voltages (i.e. with zero current) have no meaning in particular (?), because the batteries didn’t have enough time to stabilize after charging.

Note that the X-axis is given in seconds here. Not minutes.

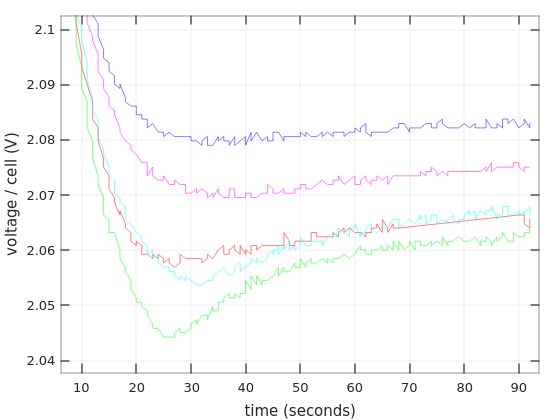
And here’s a close-up on the same graph, just to make the point that the undershoot occurred on all curves:

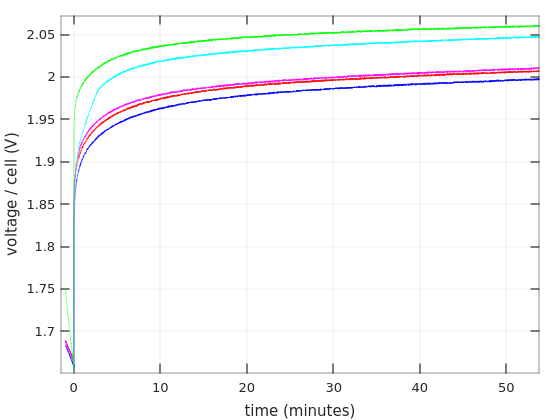
The next thing to look at is what happens when the discharging process is stopped. I did this by disconnecting the light bulb, so the current went down abruptly from 3.5A to zero. This occurs at time zero of the following graph.

Recall that Afik #2 (cyan) went down as low as 1V/cell, and yet it recovered quite similarly Afik #1, which didn’t go through this minor trauma.

It’s a well-known fact that lead-acid batteries recover after a high-current discharge and resume their capability to provide energy, even if they aren’t charged inbetween. This graph shows this phenomenon.

It’s worth looking at the first couple of minutes of the recovery. This is just a zoom-in of the previous graph (and with time axis shown in seconds instead).

Aside from the immediate jump of the voltage when the light bulb is disconnected, there’s a smooth and yet fast rise in the voltage.

Another thing that is evident from this graph, is how much faster the Afik batteries went down towards the 1.67V level, compared with the Vega Power batteries (this refers to the time period before zero).

Is a DC test legit?

This test is made with a DC current, but the UPS discharges the battery with an alternating current: As the UPS feeds the computer with an AC voltage, the delivered power as a function of time is a more or less a sinus function (if the UPS produces a sinus wave). At any time, the energy that is delivered to the computer is drawn from the battery. The UPS barely stores any energy in its own circuits. So the current from the battery is also a sinus, more or less.

So does a test with a DC current reflect the situation with an alternating current? Is it good enough to rely on the average power, and derive a DC current from that? According to Okazaki et al. (“Influence of superimposed alternating current on capacity and cycle life for lead-acid batteries“) the rippled current doesn’t change the battery’s capacity at all. They tested a current of I=I₀(1+sinωt) at 0.1Hz to 4 kHz and found only negligible differences (1%). So the DC current test seems to be accurate.

Linear discharge curve?

I’m going back to Vega Power’s second graphs, where I aligned three graphs by shifting them in the X axis. Let’s look at this graph again, but now with a dash-dotted line which represents the first-order linear regression of the segment between 20 and 40 minutes:

So there’s no doubt that the Vega Power batteries’ voltage went down linearly as a function of time for a while. Maybe it was the divergence from this linear descent that made the UPS panic after 28 minutes (once again, the UPS drew a higher current).

Looking at Afik’s curves, they don’t appear linear at any stage. Maybe that’s why the UPS became nervous very soon, but then nothing dramatic happened, so it kept running.

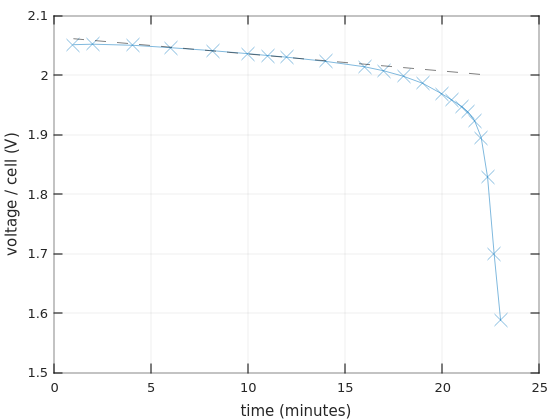
What about the Bulls Power battery? I didn’t show the graph with linear time scale above, but here it is:

Once again, the linear regression is shown with a dash-dotted line. There are fewer measurement points, but it’s quite clear that the voltage descends linearly for a while.

The slopes of these dash-dotted lines are -2.09 mV/minute for the Vega Power batteries, and -2.86 mV/minute for Bulls Power.

What’s the explanation for this linear behavior? Reiterating that lead-acid batteries is not my expertise, I’ll give it a shot:

At the first stage of discharging, the voltage curves seem to be governed mainly by the concentration of sulfuric acid close to the lead plates. As the acid is consumed by the discharging process, the supply of new acid depends on motion of ions between the two plates. A high current means a quick rate of consumption that works against the motion of ions, some of which depends on plain diffusion. So the result is a lower concentration of acid, hence a lower voltage. This, I suppose, explains why the curves go down faster for higher currents, and why the battery recovers quickly afterwards.

But here’s the thing: When the current is constant, the gradient of the sulfuric acid’s concentration stabilizes inside the cell after a few minutes. The motion of ions gets into a stable pace. However, as the current flows, sulfuric acid is consumed. This brings down the concentration of acid overall, even though the differences (gradients) remain the same. The current is constant, and the sulfuric acid is consumed against electrical charge that passes through the battery, so we have a linear slope.

At some point, the curve breaks off from this pattern, and begins diving faster. A possible reason is that the lead plates begin to lose effective surface area (blocked by lead sulfate?), so the current needs to go through a smaller surface. This is equivalent to a larger current, with the due implications on voltage drop.

This seems to be what is often referred to as “deep discharge”. This is a term that is loosely used with reference to drawing too much charge from a battery. Everyone seems to agree that this phase reduces the battery’s capacity on the following cycles, but when does it start? Is it when the curve diverges from the linear pattern? Or when the voltage gets to the level that the manufacturer suggests avoiding?

Academic material on the topic is also scarce (for example, this paper), but it seems like this phase occurs when the lead plates start to take their impact. As evident from the graphs shown above, this phase is rather unpredictable. Even though lead-acid batteries are said not to have a memory effect, that seems to be true until it comes to the lead plates themselves. They remember.

It looks like Smart UPS takes the linear slope approach. Or maybe it looks at the slope of the voltage as a function of time. As long as sulfuric acid is consumed, it’s OK, but when the lead plates begin to deteriorate, that’s time to beep like crazy. This strategy makes a lot of sense for a long battery life, but less beneficial when power outages are rare, so who cares if the battery gets a small hit every few months. But all this is my speculation on how the UPS makes its choices.

Afterthoughts

So what have I learned from all this messing around with the batteries? Not a whole lot of relevant information, I’m afraid. Invented in 1859, lead-acid batteries are easy to manufacture and easy to use, but there doesn’t seem to be a simple theory that accurately describes their behavior. As my own anecdotal experiments show, even the same battery won’t repeat its own discharging curve twice.

Maybe it was because I tried low-quality batteries (or are they?) and inaccurate apparatus for charging the batteries (the Mustek UPS). On the other hand, it’s difficult to find written material that describes the behavior of these batteries, even under lab conditions.

The state of car batteries is often tested by measuring the “cranking current”. This is the huge current when the car is started. This is a crude and indirect measurement of the lead plates’ resistance, which I suppose gives some indication of the battery’s condition. Does it ensure that your battery will hold for the next 12 months? Good luck with that.

Startup idea

The main conclusion from all this rambling is that the only way to know how long a battery will supply power is to fully discharge it. That is, down to a reasonable level that doesn’t harm it. On the other hand, a UPS should be able to give an accurate estimate of how long time it can hold up the computer, so that its user can decide when it’s time to replace the battery or batteries. Plus, the UPS needs to know this for the purpose of shutting down the computer gently a few minutes before it’s game over.

Smart UPS has a feature called “calibration” which does exactly that: It puts the computer on the batteries and discharges them until they reach the lowest acceptable level, and then resumes normal operation. The problem is that if the main power goes out at that moment, there’s nothing to hold up the computer with. So this has to be initiated by the user every now and then.

Solution: Make a UPS with say, four batteries, each of which is connected independently to the UPS’ power conversion circuitry. This way, the UPS can initiate a full discharge test on one of these batteries while the others remain fully charged. At the worst moment, the overall capacity will stand at 75%.

These discharge tests can be initiated automatically by the UPS for each of the four batteries every couple of weeks or so. This way, the UPS can give an accurate number for how long the UPS will hold up power.

This allows the user to decide when it’s time to replace the batteries. It also makes it possible to replace the batteries gradually, without turning off power. And the UPS can also inform the user if the new battery was worth the money.

Will this startup work? I doubt it. The vast majority of people just buy a UPS and believe it will do the work. They realize their mistake when the power goes out for more than two minutes, and buy a new UPS instead. Replacing lead-acid batteries separately? Come on.