PCB layout: Selecting the track width and spacing for a differential signal
Introduction
Even though this is definitely not my expertise, I made a simple adapter board carrying USB 3.0 signals.
The name of the game with such boards is to make a minimal impact on the signals, which means, among others, selecting the attributes of these two pairs of differential lines (SSRX and SSTX) in a way that minimizes the damage their very existence causes.
The other name of the game is to minimize the financial damage by ensuring that the board can be manufactured everywhere and by everyone, in particular those low-cost services.
There are a lot of things to be aware of, and I suggest reading application notes of devices that deal with the relevant type of signals. For example, TI’s board design guidelines for one of their SuperSpeed USB related devices, sllu149e.pdf.
This post focuses on selecting the track width (W) and spacing between the two differential pairs (S) of a coupled microstrip line. This is the widely recommended way to carry RF-frequency differential signals on a PCB, and it simply means that the two wires are routed at one of the exposed layers (top or bottom), and that there’s a ground plane layer immediately underneath it. See drawing at the bottom left of the image below.
Quite interestingly, there is little relation to the W and S of the differential pair in most application notes, so it’s not all that clear what considerations should be made. However, it’s well-known that W and S influence the differential impedance, and this is mentioned everywhere. The USB 3.0 specs requires the differential characteristic impedance to be 90Ω ± 7Ω in section 5.6.1.1.1. So there’s a start.
Assumptions on the PCB
These are the attributes of the most typical PCB one can find (and therefore hopefully low-cost to manufacture):
- Board material: 1 oz copper (0.035 mm thick) on FR4 resin
- Minimal track width: 10 mil. I’m generous here, as several low-cost manufacturers offer as low as 4 mil, but 6 mil is often the minimum for the lowest price. Often there’s a remark saying “>8 mil recommended”. So this indicates what’s considered easily manufactured.
- Minimal spacing between tracks: 10 mils, exactly for the same reasons. Manufacturers tend to give the same figures for both.
- Vias: I didn’t have any (on the differential pairs, that is).
The PCB calculator
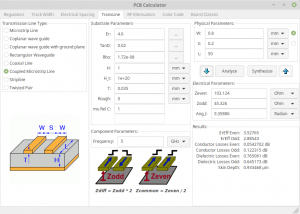
There are plenty of online calculators and other utilities for calculating the impedance of microstrip pairs. Since I used KiCad 5.1.4 for the PCB design, I also went for its PCB calculator (image of screenshot below). It’s not the easiest one however.
Quite obviously, the board’s parameters are on the left column, and the track’s data to the right. So let’s start with the board’s parameters. Note that the “…” to the right allows selecting materials instead of feeding numbers, and guess what, they’re correct (at least those related to my board).
- Er: Select FR4, and the dialectric constant is set correctly to 4.6.
- TanD: Select FR4 here as well, and don’t bother that it’s not accurate (because of the frequency): It doesn’t influence the impedance, but the only the loss calculation.
- Rho: Select copper. It’s resistivity is correct.
- H: The height to the ground plane. In my case, it’s a dual-layer board, so the ground plane is the back side. Hence H is the thickness of the entire board, 1 mm.
- H_t: The height to the ground plane (?) above the board. Luckily, doesn’t have much influence on the impedance unless it’s really small.
- T: The strip thickness. 0.035 mm for 1 oz.
- Conductor roughness: Irrelevant for impedance calculation, but will influence conductor loss calculations
- Relative permeability of conductor: Set to 1 for copper. Copper’s relative permeability, according to Wikipedia, is 0.999994, and this has no influence on impedance calculations.
- Frequency: For a USB 3.0 link, I set it to 5 GHz. Its influence on the impedance is quite small, so no need to be worried about the idea that a digital signal isn’t really band limited and such.
OK, so now what?
The goal is to find W and S. To the right, there’s also L, the length of the trace. It has no influence on the impedance, so any positive number goes. Likewise, we don’t care about the electrical length (Ang_l) which basically says how much delay, in terms of sinusoidal phase of the given frequency, the conductor imposes.
So there are two input parameters, W and S, and two output parameters, Zeven and Zodd. As the signal is differential with no common mode component, we don’t care about Zeven at all: Since Zdiff = Zodd * 2, we just need to make Zodd = 45Ω, more or less.
Or in other words, there is one degree of freedom. There isn’t one pair of W and S for a given board and impedance, but we get to select one of them.
So the rather silly methodology is to pick some initial W and S, more or less at random, and click the down arrow (or “Analyze”). See what we got. Then set Zodd to 45, and click the up arrow (or “Synthesize”). And then some manual iteration, until the result is fine.
But that leaves us with the need to make a decision.
What is a good pair of W and S?
To make a long story short, as small as possible. These wires aren’t carrying any significant currents, so their size is only limited by the manufacturing process (or: How much we’re ready to pay for it). For low-cost manufacturing, consider that they sometimes make the trace thinner by a mil or two (this is the low-quality side of low-cost). So it’s important to be aware of how this would impact the impedance.
Why is small good? Mainly for crosstalk and noise immunity: The closer the wires are to each other, the more do they behave as a differential pair. Being closer to each other, noise signals are added more equally, leading to a smaller differential noise signal. A common rule of thumb is that a differential pair should have a clearance of 5W from any other conductor.
It’s also a matter of taking up less physical space on the board (in particular when respecting the 5W rule above).
As for signal losses, it doesn’t seem to make a big difference.
There is however no defined way to iterate with the calculator to obtain good values. One may select a minimal W and try out several S until Zodd is 45Ω, but it may be below the minimal S allowed.
In that case, start with the minimal S, and increase W until Zodd is 45Ω. If we want to follow the 5W rule, that is probably the best pair achievable.
As for my own choice, it’s the one shown in the image above: W = 0.8 mm, S = 0.2 mm. This makes S a bit smaller than 8 mils. Even though me original intention was not to go below 10 mils, this settings allows me to meet the 5W rule. And it should still be fine to manufacture virtually anywhere.
These rather bulky tracks weren’t easy to connect to the USB receptacle’s footprint, as discussed in another post.
Other calculators
Given the importance of getting these figures right, it’s reassuring to feed the results into other calculators before etching them in metal.
Note that some calculate Zodd and some give you the differential impedance (plus, possibly some other figures). Don’t get confused, and no panic.
- Multi-Teknik’s calculator is much simpler, and also shows the formula.
- Everything RF, also showing the formulas.
- EEweb is more like the PCB calculator (i.e. requires some brain) and shown more math that you probably want to know about.
- All About Circuits is also on the heavier part with the math.